Dekomposisi Matriks dengan Metode Doolittle
Suatu persamaan linear dapat diselesaikan secara langsung. Salah satu caranya adalah dengan menggunakan dekomposisi LU. Pada metode ini suatu sistem persamaan linier yang berbentuk:
difaktorisasi menjadi:
Pada dekomposisi LU metode Doolittle, semua komponen diagonal matriks L bernilai 1 sehingga representasi matriks di atas menjadi:
Untuk menghitung setiap komponen matriks L dan U dari matriks A dengan ukuran n x n dapat dengan menggunakan algoritma sebagai berikut:
1. Dapatkan nilai matriks U pada baris pertama:
untuk i = 1 sampai n
2. Hitung nilai:
untuk i=2 sampai n
3. untuk i = 2 sampai n-1
untuk j = i + 1 sampai n
4. Hitung indeks terakhir:
Proses dekomposisi selesai sampai disini, proses berikutnya adalah untuk menyelesaikan sistem persamaan linier nya.
Dari dekomposisi berikut:
Matriks L dan U sudah kita dapatkan, dan dengan memisalkan:
maka
untuk mendapatkan nilai vektor y dapat dilakukan dengan substitusi maju sebagai berikut:
untuk i=2 sampai n
nilai vektor x didapatkan dengan melakukan substitusi mundur persamaan:
dengan cara:
untuk i=n-1 sampai 1
Selesai!!Sistem persamaan linier tersebut sudah dapat diselesaikan, dengan catatan:
matriks harus square.
tidak ada komponen diagonal bernilai nol (jika ada yang bernilai nol harus dilakukan pertukaran baris terlebih dahulu).
Sumber: Burden R.L., Faires J.D. Numerical analysis (7ed., Brooks Cole, 2001)



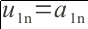








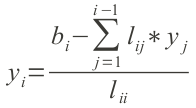






Tidak ada komentar:
Posting Komentar